División de polinomio por el método de Horner
Para continuar este apartado de división algebraica ahora se presenta un método alternativo para dividir polinomios de manera abreviada el cual a diferencia de la regla de Ruffini no requiere que el divisor sea un polinomio lineal.
El método de Horner es llamado así en honor a William George Horner y se dice que era ya conocido por Newton y por otros matemáticos. Algunos afirman que la primera aparición de este método se dio en el libro matemático “Los nueve capítulos sobre arte matemático” (la traducción al texto puede variar), el cual es datado antes del nacimiento de Cristo.
Dado un polinomio en forma estándar y completo, $$P\left(x\right)=a_mx^m+a_{m-1}x^{m-1}+a_{m-2}x^{m-2}+\cdots+a_1x+a_0$$ entonces el cociente y residuo de dividir \(P\left(x\right)\) entre cualquier polinomio \(d(x)\) de grado \(n\) en forma estándar, tal que \(n< m\) pueden obtenerse mediante los siguientes pasos.
\(1.\) Escribir en forma vertical los coeficientes del divisor \(d(x)\) con signos cambiados, excepto el coeficiente principal y escribir en forma horizontal (como en la regla de Ruffini) los coeficientes de \(P(x)\) en formato de tabla, separando las últimas \(n\) columnas las cuales representaran el residuo \(r(x),\) donde \(n\) es el grado del divisor \(d(x).\)
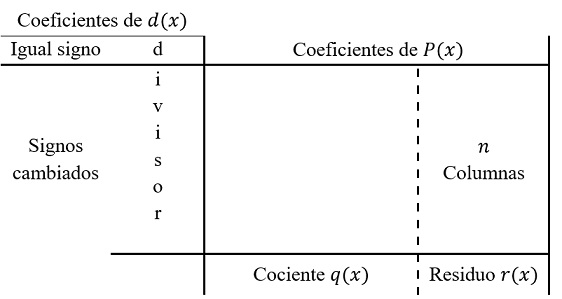
\(2.\) Dividir el coeficiente principal de \(P(x)\)entre el coeficiente principal de \(d(x),\) este resultado es el primer coeficiente del cociente \(q(x).\)
\(3.\) Multiplicar este cociente por los coeficientes de \(d(x)\) que cambiaron de signo (desde arriba hacia abajo) escribiendo los productos debajo de los coeficiente de \(P(x)\) correspondiente a la columna inmediata a la derecha y simplificar.
\(4.\) Dividir el resultado de la segunda columna entre el coeficiente principal de \(d(x),\) este resultado es el segundo coeficiente del cociente \(q(x)\) y realizar el paso anterior con el valor encontrado.
\(5.\) Repetir los pasos tres y cuatro tantas veces como coeficientes hayan antes de la línea vertical que separa al cociente del residuo (se divide hasta aquí).
\(6.\) Escribir los polinomios cociente y residuo, donde el grado del cociente es \(m-n\) y el del residuo está dado por el grado al cual pertenece la columna de su coeficiente principal.
Ejemplo 1. en el último de los ejemplo de la regla de Ruffini se realizó la división de \(P(x)=3x^4+12x^3-15x^2+6x+120\) entre \(3x+6,\) ahora se presenta su resultado por el método de Horner.
Solución: los polinomios están en forma estándar y completos, así que se puede aplicar el método de Horner. El formato de tabla es como sigue.
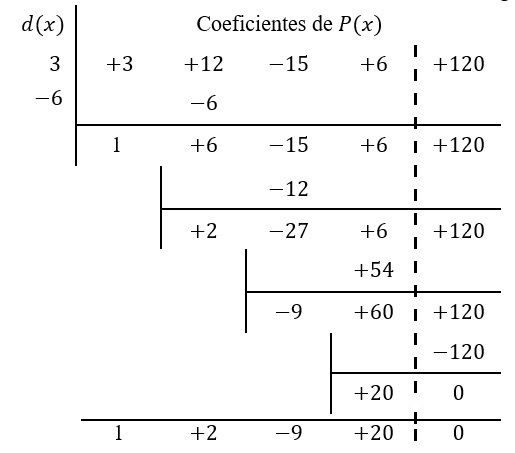
¿Qué es lo que se ha hecho para llegar hasta aquí?
Paso 1. Dividir el primer coeficiente de \(P(x)\) entre el primer coeficiente de \(d(x)\), esto es \(3\div3=1\) que es el primer coeficiente del cociente \(q(x)\).
Paso 2. Multiplicar \(1(-6)=-6\) y escribir el resultado en la columna inmediata a la derecha, simplificando \(12-6=6,\) escribiendo los demás valores iguales.
Paso 3. Dividir \(6\div3=2\) (segundo coeficiente de \(q(x)\)) multiplicar \(2(-6)=-12,\) escribir en la columna de la derecha simplificando \(-15-12=-27.\)
Paso 4. Dividir \(-27\div3=-9\) (tercer coeficiente de \(q(x)\)), multiplicar \(-9(-6)=54,\) y simplificar \(6+54=60.\)
Paso 5. Dividir \(60\div3=20\) (cuarto coeficiente del cociente \(q(x)\)) con la cual se ha llegado a la línea divisoria del cociente y el residuo, por tanto, esta es la última división, multiplicar \(20(-6)=-120,\) escribir el resultado en la columna inmediata a la derecha y simplificar \(120-120=0.\)
Paso 6. Escribir los polinomios \(q(x)\) y \(r(x).\) Para el grado de \(q(x)\) se realiza la resta de los grados del dividendo y el divisor, \(m-n=4-1=3\) de donde \(q(x)=x^3+2x^2-9x+20.\) El residuo \(r(x)=0\).
Ejemplo 2. Dividir \(3x^4+19x^2+5x+10\) entre \(x^2+6\) mediante el método de Horner.
Solución: para aplicar el método los polinomios deben estar en forma estándar y completo, así que se escribe \(3x^4+0x^3+19x^2+5x+10\) entre \(x^2+0x+6,\) y se procede como en el ejemplo anterior donde por ser el divisor de grado dos, las últimas dos columnas de la tabla son \(r(x).\)
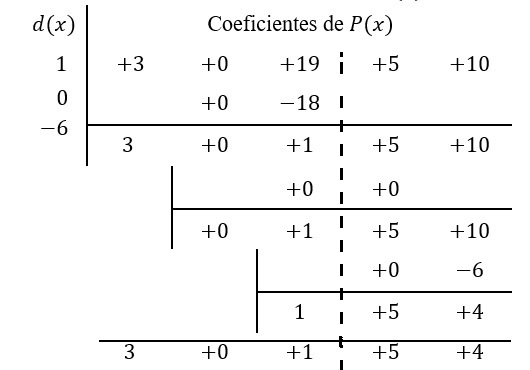
De donde se concluye que como \(m-n=4-2=2\) el cociente es, \(q\left(x\right)=3x^2+0x+1=3x^2+1.\) Como \(d(x)\) es de grado dos el residuo son las últimas dos columnas, \(r\left(x\right)=5x+4\) por estar el coeficiente cinco en la columna de \(x^1=x\) con respecto de los coeficientes de \(P(x).\)
Como se puede notar este es un resultado no era posible de determinar mediante regla de Ruffini, obligando a realizar división larga y por este método resulta sencillo. Realice la comparación entre los métodos y verá que la regla de Ruffini es un caso especial del método de Horner, sin embargo en ninguna se pretende quitar mérito o alegar copiado de una regla a otra.
Ejemplo 3. Dividir mediante el método de Horner el polinomio \(P(x)=x^5-3x^4+x^3-3x^2-2x+6\) entre \(d(x)=x^2+2.\)
Solución: comenzando por escribir los polinomios en forma estándar y completos, \(P(x)\) está ordenado y completo. \(d(x)=x^2+0x+2\) y procediendo como en los ejemplos anteriores las últimas dos columnas de la tabla serán el residuo.
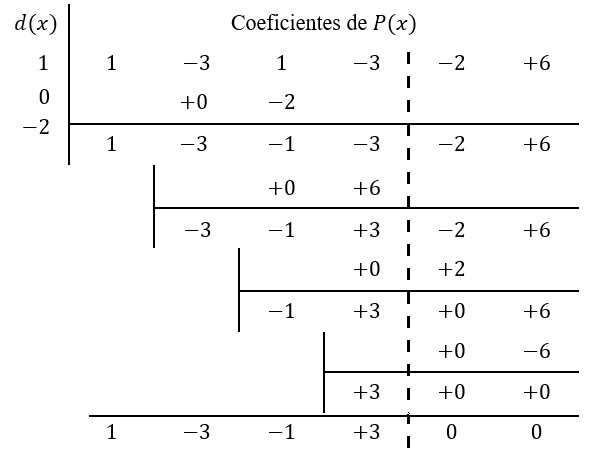
De donde el cociente \(q\left(x\right)\) es de grado \(m-n=5-2=3\) de entonces \(q(x)=x^3-3x^2-x+3\) y el residuo \(r(x)=0.\)
Ejemplo 4. Dado el polinomio \(P(x)=x^6+3x^4+6x^2+10\) dividirlo entre \(d(x)=x^4+5\) mediante el método de Horner.
Solución: como el divisor \(d(x)\) es de grado cuatro, el residuo \(r(x)\) será el resultado de las últimas cuatro columnas. Además completando los polinomios se observa que \(P(x)=x^6+0x^5+3x^4+0x^3+6x^2+0x+10\) mientras que el divisor \(Q(x)=1x^4+0x^3+0x^2+0x+5\) de esto se tiene,
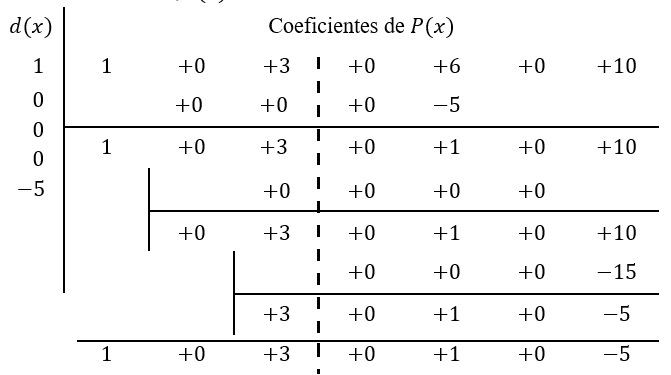
De donde \(q\left(x\right)=1x^2+0x+3=x^2+3\) y \(r(x)=1x^2-5=x^2-5\)
Para más contenidos y luego clic en la pestaña del contenido deseado.
Regla de Ruffini o división sintética.
Si \(P\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\ldots+ax+a_0\) es un polinomio racional y \(Q\left(x\right)\) es un binomio de la forma \(Q\left(x\right)=mx-c\) o \(Q\left(x\right)=mx+c\) la división \(\frac{P\left(x\right)}{Q\left(x\right)}\) puede realizarse de manera abreviada como sigue:
1. Ordenar de manera descendente \(P\left(x\right)\), completando con ceros (si es necesario) los términos de los grados faltantes para que \(P\left(x\right)\) esté completo y ordenado.
2. Escribir en una fila los coeficientes de \(P\left(x\right)\) ya ordenado y completo con sus mismos signos.
3. Si \(Q\left(x\right)=mx-c\) tomar \(\frac{c}{m}\) y si es de la forma \(Q\left(x\right)=mx+c\) tomar \(-\frac{c}{m}\) y realizar operaciones de multiplicación y sumas aritméticas en la siguiente manera:
3.1. Se toma el valor del coeficiente principal \(a_n\) y se multiplica por \(\frac{c}{m}\) y se suma con \(a_{n-1}\).
3.2. La suma encontrada denotada por \(s_1\) se multiplica \(\frac{c}{m}\) y se suma con \(a_{n-2}\).
3.3. Llamando al resultado \(a_{n-2}+s_1\left(\frac{c}{m}\right)=s_{2}\) se repite el procedimiento hasta llegar a \(a_0\).
$$\begin{array}{r| c c c c c}
&a_n &+a_{n-1}~~~~&+a_{n-2}~~~~~&+~~\cdots&+a_0~~~~~~~~~~~~\\
c/m&\Downarrow & +a_n\left(\frac{c}{m}\right)&+s_1\left(\frac{c}{m}\right)&+~~\cdots&+s_{n-1}\left(\frac{c}{m}\right)\\
\hline & a_n &s_1~~~~~~~&s_2~~~~~~&s_{n-1}&\textcolor{#ff0080}{r(x)}~~~~~~\end{array}$$
4. Si \(m=1\) los coeficientes del cociente \(q(x)\) son el resultado de la última fila sin el valor de la última columna que es el residuo \(r(x)\) de la división, siendo \(q(x)\) un grado menor que \(P(x)\).
Si \(m\neq1\) se deben dividir los coeficientes de la última fila entre \(m\) para tener el cociente \(q(x)\) con su valor real. El residuo \(r(x)\) no cambia.
Ejemplo 1. Dividir \(x^4-4x^2+8x-2\) entre \(x-2\)
Comience por escribir \(P(x)=1x^4+0x^3-4x^2+8x-2\) para que esté ordenado y completo, \(Q(x)=mx+c=1x-2\) de donde \(m=1\).
Coloque en una tabla los coeficientes de \(P(x)\) y realice las operaciones como se indicó en los pasos anteriores, de done se tiene:
$$\begin{array}{r| r r r r r}
&1 &0 &-4&+8&-2\\
2&\Downarrow & 1(2)=2&2(2)=4&0(2)=2&8(2)=16\\ \hline
&1& +2 &+0&+8&\textcolor{#ff0080}{14}\end{array}$$
Como \(m=1\) se tiene que \(q(x)=1x^3+2x^2+0x+8\) \(\Longrightarrow \ q(x)=x^3+2x^2+8\). Recuerde que \(q(x)\) es un grado menor que \(P(x)\), por tanto, como \(P(x)\) es de grado cuatro \(q(x)\) es de grado tres.
Por el teorema del residuo como
\(r\left(x\right)=\textcolor{#ff0080}{14}\) entonces \(x-2\) no es factor de \(P(x)\).
Ejemplo 2. Dividir mediante división sintética.
\(P(x)=x^3-64\) entre \(x-4\). Usar el resultado para saber si es \(x-4\) factor de \(x^3-64\).
\(P(x)=1x^3+0x^2+0x-64\) y \((Q(x)=mx+c=1x-4\) de donde se tiene:
$$\begin{array}{r| r r r r}
&1 &+0 & +0&-64&\\
4&\Downarrow & 1(4)=4&4(4)=4&16(4)=64&\\ \hline
&1& +4 &+16&+\textcolor{#ff0080}{0}&\end{array}$$
\(r\left(x\right)=\textcolor{#ff0080}{0}\) por tanto, por el teorema del factor \(x-4\) es factor de \(P(x)\).
Como \(m=1\) se tiene que \(q(x)=1x^2+4x+16 \Longrightarrow\ q(x)\)=x^2+4x+16\)
NOTA: a partir del próximo ejemplo los productos se escribirán de forma directa.
Ejemplo 3. Dividir \(2x^6+13x^5-9x^4+1/8\) entre \(2x-1\).
$$\begin{array}{r| r r r r r r l} &2 &+13 & -9&+0&+0&+0&+1/8&\\ 1/2&\Downarrow & +~~1&+7&-1&-1/2&-1/4&-1/8&\\ \hline &2& +14 &-2&-1&-1/2&-1/4&~~~~\textcolor{#ff0080}{0}\end{array}$$ \(r\left(x\right)=\textcolor{#ff0080}{0}\) por tanto, por el teorema del factor \(x-\frac{1}{2}\) es factor de \(P\left(x\right)\). Como \(m=2\) se debe dividir los coeficientes del cociente obtenidos por dos y se tiene: $$ q(x)=x^5+7x^4-x^3-\frac{1}{2}x^2-\frac{1}{4}x-\frac{1}{8}$$ Ejemplo 4. Dividir \(3x^4+4x^3-4x^2+2x+4\) entre \(3x+6\) $$\begin{array}{ r| r r r r r} &3&+4&-4&+2&+4\\ -2&\Downarrow &-6&+4&+0&-4\\ \hline &3&-2&0&2&\textcolor{#ff0080}{0}\end{array}$$ Como \(m=3\) en \(Q(x)=3x+6\) se debe dividir los coeficientes de \(q(x)\) por tres, y se tiene: $$q(x)=\frac{3}{3}x^3-\frac{2}{3}x^2+0x+\frac{2}{3}\Longrightarrow q\left(x\right)=x^3-\frac{2}{3}x^2+\frac{2}{3}$$ Como \(r\left(x\right)=\textcolor{#ff0080}{0}\) por el teorema del factor \(x+2\) es un factor de \(P\left(x\right)\).
Para más contenidos y luego clic en la pestaña del contenido deseado.
Dividir mediante división sintética \(P\left(x\right)=x^3-64\) entre \(x-4\). Usar el resultado para saber si es \(Q(x)=x-4\) factor de \(x^3-64\)
Verificar si los binomios \(Q_1\left(x\right)=2x-3\); \(Q_2\left(x\right)=4x-1\) y \(Q_3\left(x\right)=x-3\) son factores del polinomio \(P\left(x\right)=8x^3+10x^2-39x+9\)
Verificar si cada uno de los binomios \(Q_1(x)=x+2\); \(Q_2(x)=x-2\) y \(Q_3(x)=x-4\) son o no factores del polinomio $$P(x)=x^4+x^3-16x^2-4x+48$$
Verificar si cada uno de los binomios \(Q_1(x)=2x+3\); \(Q_2(x)=2x-1\) y \(Q_3(x)=x+1\) son o no factores de \(P\left(x\right)=4x^3+8x^2+x-3\), si lo son, escribir el polinomio como un producto.
El área de un terreno rectangular está dada por la expresión \(A=4x^2-9\). Si se sabe que el largo es \(l=2x+3\) determine la medida del ancho \(w\).
